评价函数与相关系数R平方
一、评价函数的核心作用
评价函数是量化交易中度量和比较策略/参数性能的关键工具。在MT5参数优化中,它决定了不同参数组合的排序逻辑(如按盈利、风险或综合指标排序)。
二、常见评价函数对比
| 指标 | 定义 | 优缺点 |
|---|---|---|
| 最大结余 max balance | 净利润总和 | 仅关注收益,忽略风险,片面性强 |
| 最大回撤 max drawdown | 净值从最高点到最低点的最大跌幅 | 仅关注风险,忽略收益,片面性强 |
| 盈利因子profit factor | 总盈利 / 总亏损(>1为盈利) | 综合收益与亏损,衡量策略盈亏比 |
| 采收率(风报比recovery factory) | 净盈利 / 最大回撤 | 风险收益比,数值越大表明单位风险回报越高 |
| 夏普比率 sharp ratio | (收益-无风险利率)/ 波动率 | 经典风险调整收益指标,需假设无风险利率 |
提示
按照每年采收率0.5来算回测10年需要达到5才算及格
三、核心主题:相关系数R平方
1. 统计学原理
- Pearson相关系数(R):衡量两个变量线性相关程度,范围[-1, 1]。
- R=1:完全正相关;R=-1:完全负相关;R=0:无线性相关。
- R平方(R²):R的平方,反映变量变异中可由线性回归解释的比例,范围[0, 1]。
2. 在资金曲线上的应用
(1)核心目标
通过线性回归拟合资金曲线,计算R²值,判断资金增长的“稳定性”与“线性程度”。理想状态是资金曲线贴近一条稳定上升的直线(R²→1)。
(2)案例分析
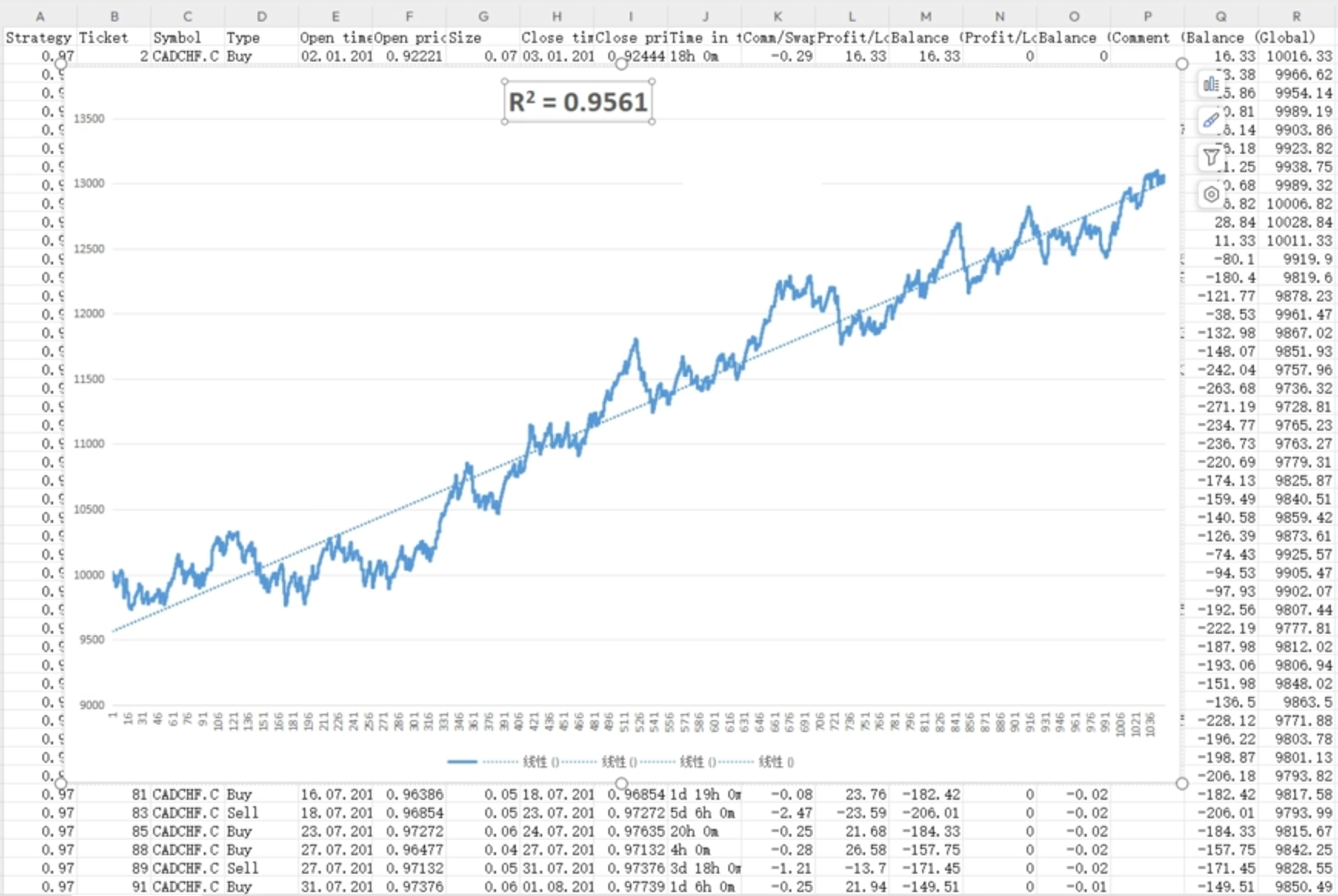
- 优质曲线:R²=0.9561,资金点紧密围绕拟合线,增长稳健。
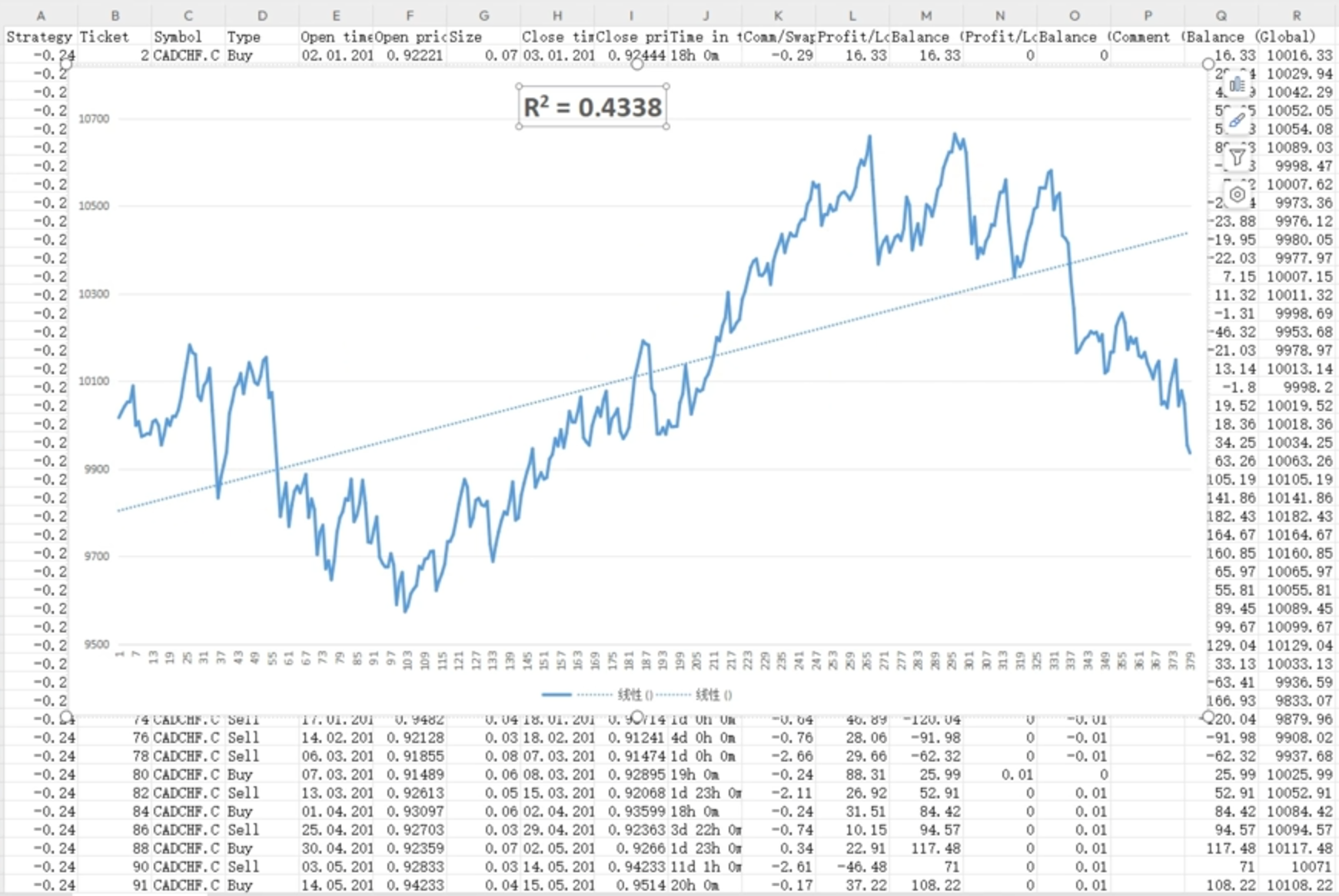
- 劣质曲线:R²=0.43,资金点分散,波动剧烈。
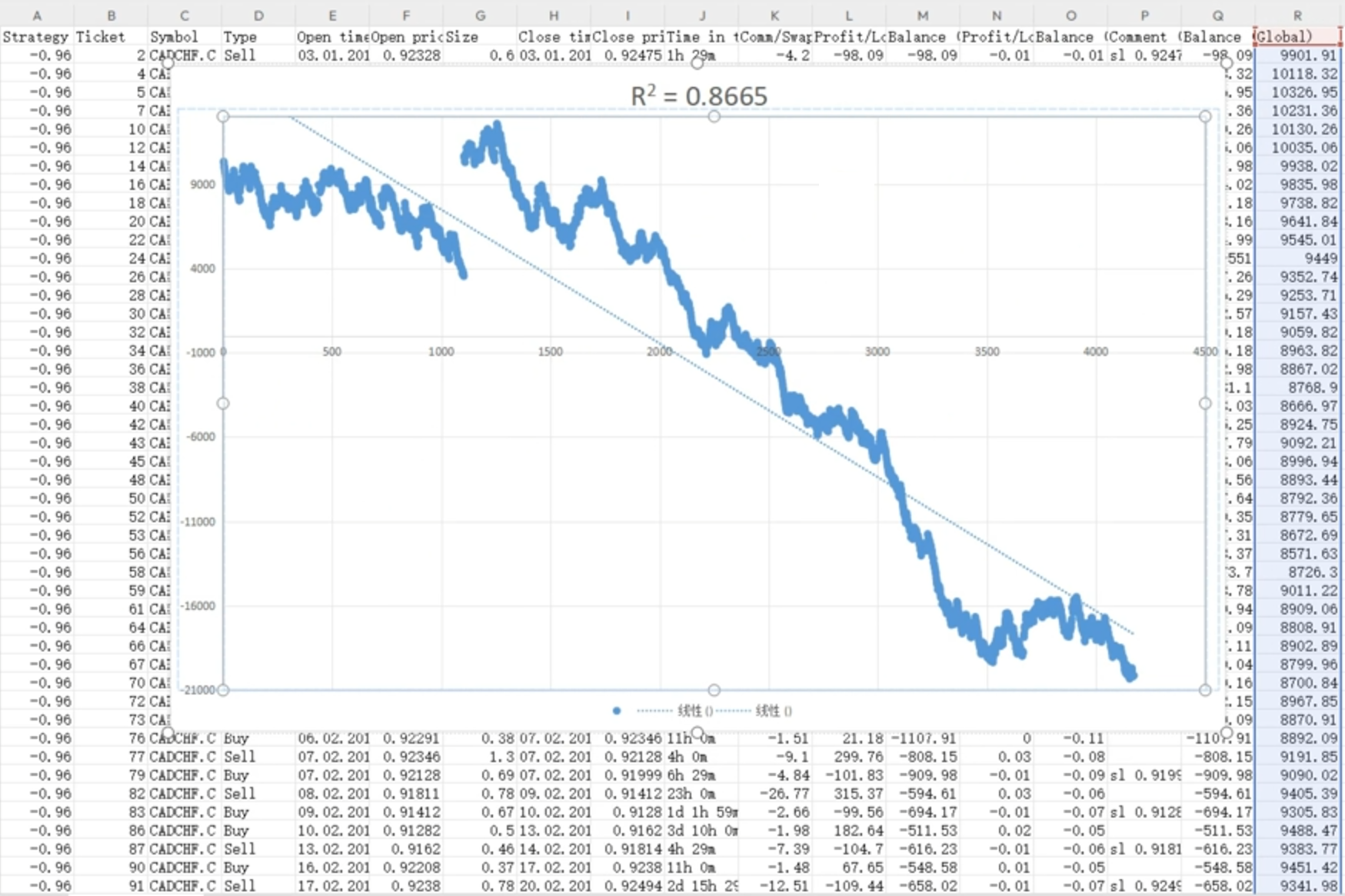
- 特殊情况:R²=0.88但为负值,表明资金稳定下跌(负相关),需排除。
二、相关系数R平方:一种独特的评价视角
1. 统计学背景
- Pearson相关系数(R):衡量两个变量线性相关程度,范围在[-1, 1]之间。
- +1:完全正相关,-1:完全负相关,0:无线性相关。
- R平方(R²):相关系数的平方,反映变量与拟合直线的贴近程度,值越接近1,线性相关性越强。
2. 在资金曲线上的应用
- 使用方法
- 用最大结余那一列绘制折线图
- 图表选中生成趋势线
- 在点击趋势线后,右侧选线显示R平方值

- 核心思想:通过线性回归拟合资金曲线,计算其与拟合直线的相关系数R²,衡量收益的稳定性和质量。
- 示例分析:
- 高R²(如0.95):资金曲线贴近直线,收益稳健(如图1)。
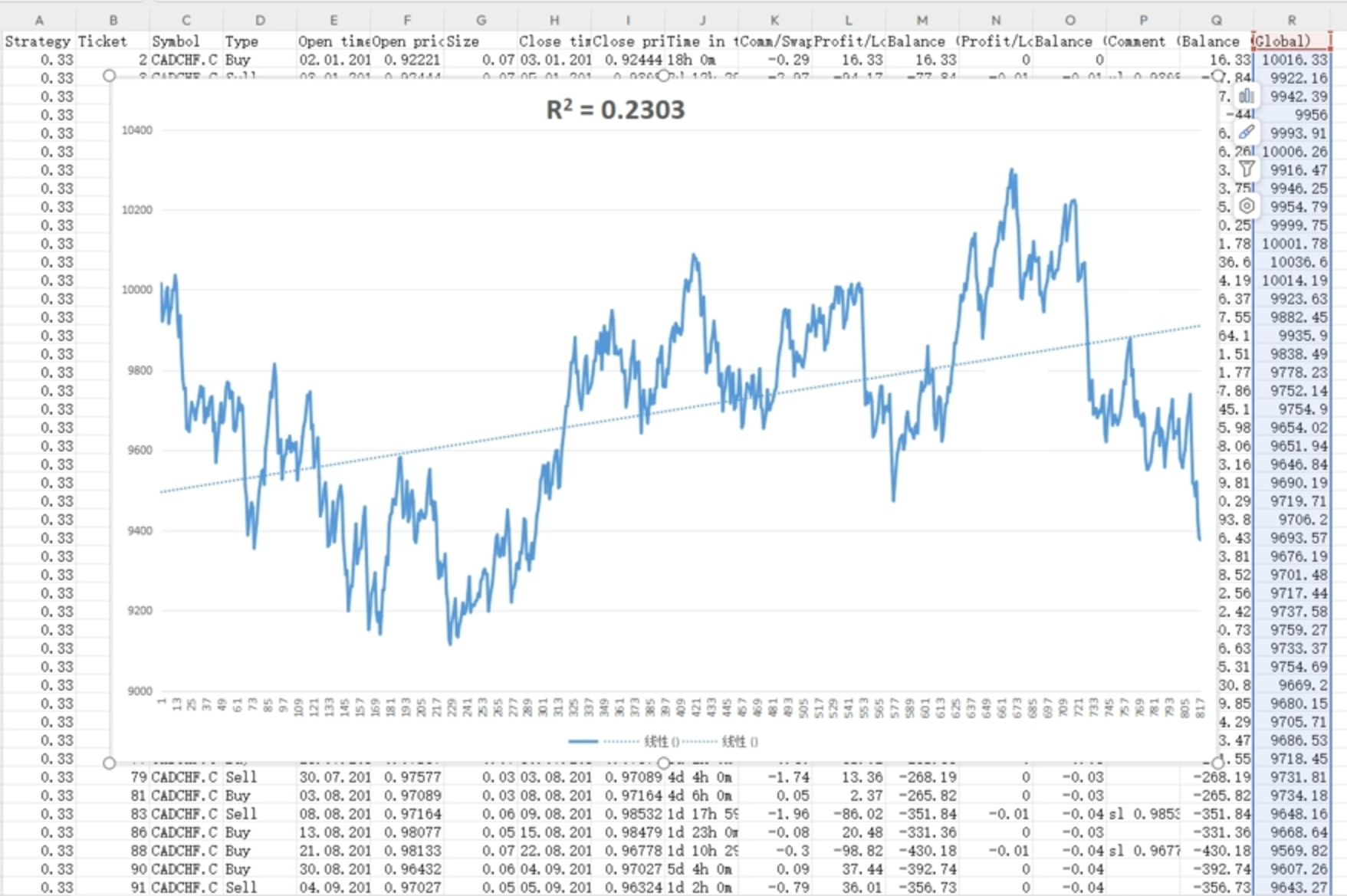
- 低R²(如0.43或0.23):曲线波动大,与直线偏离度高(如图2,图3)。
- 负R²(如-0.86):资金曲线稳定下降,呈现负相关(如图4)。
3. 使用注意事项
- 仓位固定:相关系数基于线性回归,要求仓位计算为固定类型(1或3模式)详情见4种仓位管理方式,避免动态仓位导致的指数型曲线干扰拟合效果。
- 交易频率:需设定最低交易笔数(如每年≥24笔),避免样本不足影响评价有效性。
三、代码实现
1. 核心逻辑
- 数据准备:记录每笔交易后的资金余额(Y轴)与交易笔数(X轴)。
- 函数调用:利用MT5内置库计算相关系数,避免手动实现复杂公式。
2. 代码示例
cpp
int OnInit(){
if(MQLInfoInteger(MQL_TESTER)){
BackTestFirstDate = TimeCurrent();
StartingEquity =AccountInfoDouble(ACCOUNT_EQUITY);
}
}
#include <Math\Stat\Stat.mqh> // Required for MathStandardDeviation()
datetime BackTestFirstDate; // 回测开始时间
double StartingEquity; // 存储起始资产余额(即回测开始的存款金额)
double OnTester(){
double customPerformaceMetric = 0.0;
int numTrades = CoeffCorrelation(customPerformaceMetric,StartingEquity);
// 1. 这是回测持续时间(以秒为单位), 但为避免下方出现问题, 需将其强制转换为双精度类型 2. "秒"转换为"年"
datetime BackTestFinalDate = TimeCurrent();
double BackTestDuration = double(BackTestFinalDate - BackTestFirstDate);
BackTestDuration = (((( BackTestDuration / 60.0) / 60.0) / 24.0 )/365.0);
double needTrades = BackTestDuration* 24; // 每年至少24笔交易
if(numTrades<needTrades)
customPerformaceMetric = 0.0;
customPerformaceMetric = NormalizeDouble(customPerformaceMetric,5);
return customPerformaceMetric;
}
//计算相关系数R,这将产生与确定系数(Coeff of Determination)相同的挂名
//相关系数R的值介于-1和+1之间。确定系数(R-Squared)只是相关系数的平方。
//因此,它的范围为@到1。但是,出于我们的目的,我们希望保留符号,以便知道资产曲线是上涨还是下跌。
//接近+1的值表示非常平艳的上涨趋势。接近-1的值表示非常平稳的下跌隐势(即非常建糕),接近8的值表示盈亏平衡的系统,具省波动的资产曲线
//例如,0.6的值表示具有波动资产曲线的盈利系统。
//交易次数(从8开始,并以1逆增)用于X值。
//系积资产值用于Y值。
//相关系数公式:
// r =( n(SLM(x))-(SUM(x))(Sum(y)))/( SORT( n(SuN(x-squared)- suM(x)squared))* SORT(n(SLM(y-squared))- SLM(y)squared))1
//r值为正表示资产曲线上涨-G00D。与+1越接近,资产曲线上涨趋势就越高效。
//r值为负表示资产曲线下跌-BAD。越接近-1,资产曲线下跌趋势也越高效。
//接近+1表示上涨趋势,接近-1表示下跌趋势,接近0表示资产曲线有波动。
int CoeffCorrelation(double &dCustomPerformanceMetric, double dStartingEquity){
//初始化两个数组,作为计算相关系数的基础数据
//数组"equityID"和"cumNormalisedNetProfit” 分配初始空间,大小设置为1
int numEquityValues =1;
double equityID[];
double cumNormalisedNetProfit[];
ArrayResize(equityID, 1);
ArrayResize(cumNormalisedNetProfit, 1);
// 使用1.0赋 初值给equityID 对应的第一个值, 也就是x值
equityID[0] = 1.0;
// 使用初始资产价值赋初值给customNormalisedNetProfit 对应的第一个值, 也就是y值
cumNormalisedNetProfit[0] = dStartingEquity;
// 循环遍历所有的历史交易记录
HistorySelect(0,TimeCurrent());
int numDeals = HistoryDealsTotal();
for(int deaID=0;deaID<numDeals;deaID++){
ulong dealTicket = HistoryDealGetTicket(deaID);
if(HistoryDealGetInteger(dealTicket,DEAL_ENTRY) == DEAL_ENTRY_OUT){
numEquityValues++;
double tradeNetProfit = HistoryDealGetDouble(dealTicket,DEAL_PROFIT)+
HistoryDealGetDouble(dealTicket,DEAL_SWAP)+
2*HistoryDealGetDouble(dealTicket,DEAL_COMMISSION);
// 获取交易的数量
double tradeVolume = HistoryDealGetDouble(dealTicket,DEAL_VOLUME);
// 数组扩充空间,存储本次交易的数据
ArrayResize(equityID,numEquityValues);
ArrayResize(cumNormalisedNetProfit,numEquityValues);
// 将交易次数存入equityID, 将归一化的资产价值加入到cumNormalisedNetProfit
// tradeNetProfit/tradeVolume 就是当前交易后的归一化资产价值, 然后它被价到上一次计算的累积资产价值上,从而的到了这一次交易后的累积资产价值
equityID[numEquityValues-1] = (double)numEquityValues;
cumNormalisedNetProfit[numEquityValues-1] = cumNormalisedNetProfit[numEquityValues-2] + (tradeNetProfit/tradeVolume);
}
}
// 初始化相关系数
double coeffOfCorrelation = 0.0;
// 使用MQL5内置函数计算pearson相关系数
if(!MathCorrelationPearson(equityID,cumNormalisedNetProfit,coeffOfCorrelation)) coeffOfCorrelation=0.0;
// 将结果相关系数值存入dCustomPerformanceMetric
dCustomPerformanceMetric = coeffOfCorrelation;
return numEquityValues-1;
}3. 优化效果
- 排序依据:参数优化时选择“最大定制”,优先筛选资金曲线贴近稳定上升直线的参数。
- 结果示例:
- 高R²(0.97):资金曲线稳定上涨,排名靠前。
- 负R²(-0.96):稳定亏损,排名靠后。
- 低R²(0.12):波动剧烈,无明显趋势,排名居中。
四、总结
相关系数R平方从统计学角度为策略评价提供了新维度,关注资金曲线的“线性稳健性”,弥补了传统指标(如单纯利润或回撤)的片面性。使用时需注意仓位固定和交易频率要求,适用于追求稳定收益的策略优化。建议结合其他指标综合评估,提升参数筛选的可靠性。